Essential Data Structures for Every Programmer
The most common data structures that you’ll get the most out of
Cover Photo by Alex Ronsdorf on Unsplash
It is quite amazing how you can go from zero to a fully professional software engineer solely with the help of free resources available on the internet. But it can also be noted that developers who take this path often disregard the concept of data structures. They believe that knowledge of these data structures wouldn’t benefit them as they’ll only be developing simple applications.
But on the contrary, I believe learning data structures, right from the start, is essential. Data structures are mainly beneficial for building efficient applications. An application built using data structures will be more efficient than an application built without them. But this does not mean that you should use data structures for each and every requirement. I personally believe that the knowledge of the application of these data structures is more important than the knowledge of the data structures themselves.
What is a Data Structure?
Regardless of your profession, your daily work involves data. Whether you are a chef, software engineer, or even a fisherman, you still work with data in various different forms.
Data structures are containers that store data in a specific layout format. This specific layout format enables the data structure to have specific qualities that differentiate itself from other data structures and makes it strong and weak for different use case scenarios.
Let’s have a look at some of the most essential data structures that can help you to build efficient solutions.
Arrays
Arrays are one of the simplest and most commonly used data structures. Data structures such as Queues and Stacks are based on Arrays and Linked Lists (which we will look into after arrays).
Each element in the array is given a positive integer that denotes the location or position of the element in that array. This value is known as the index. Indexes start from zero in most languages and this concept is called zero-based numbering/indexing.
There are two types of arrays. They are one-dimensional arrays and multi-dimensional arrays. One-dimensional arrays are the simplest of arrays as they are linear. But multi-dimensional arrays are nested arrays which are basically arrays containing arrays.
Basic array operations
Get— get the array element at the given index.Insert— insert an array element at the given index.Length— get the number of elements in a given array.Delete— remove an array element at the given index. This can be performed either by making the element value as undefined or by copying the array elements excluding the element to be removed to a newer array.Update— update the value of an array element at the given index.Traverse— loop through the array to perform functions on array elements.Search— find a specific element on a given array by using a search algorithm of choice.
Applications of arrays
Arrays are the building blocks of more advanced data structures like stacks, queues, etc.
Arrays are generally used for simple storage of related data. This is mainly because of their ease of use.
Arrays are also used for different sorting algorithms such as insertion sort, bubble sort, etc.
 One dimensional array
One dimensional array
 Two-dimensional array
Two-dimensional array
Linked List
A Linked list is simply a collection of elements called nodes, in a linear sequential structure. A node is a simple object with two properties. These are variables to store data and to store the memory address of the next node in the list. Therefore, a node only knows about what data it contains and who its neighbor is. This makes way for the creation of linked lists where each node is chained to the other.
 Source: Educative.io
Source: Educative.io
There are several types of linked lists.
Singly linked list: Traversal of items can be done in the forward direction only.
Doubly linked list: Traversal of items can be done in both forward and backward directions. Nodes consist of an additional pointer known as prev, pointing to the previous node.
Circular linked lists: Linked lists where the previous (prev) pointer of the head points to the tail and the next pointer of the tail points to the head.
Basic LinkedList operations
Insertion: Add a node to the list. This can be done based on the required location such as the head, tail, or somewhere in between.Delete: Delete a node at the beginning of the list or based on the given key.Display: Display the complete list.Search: Search for a node within the given LinkedList.Update: Update the value of a node at a given key.
Applications of linked lists
Similar to arrays, linked lists are used as building blocks of advanced data structures such as queues, stacks, and some type of graphs.
Used in image slideshows as each image is chained to one another.
Used in dynamic memory allocation structures.
Used in operating systems to switch tabs easily.
You can read more about linked lists in my article here.
Stack
A stack is a linear data structure that is created based on either arrays or linked lists. A stack follows the Last-In-First-Out (LIFO) principle, in which the last element to enter a stack, will be the first to leave. The reason this data structure is called a stack is that this layout resembles a real-world stack — you can visualize it as a stack of books on a table.
 Photo by Prateek Katyal on Unsplash
Photo by Prateek Katyal on Unsplash
Basic stack operations
Push: Insert an element to the top of the stackPop: Remove the element from the top of the stack and return it.Peek: View the element at the top of the stackisEmpty: Check whether the stack is empty
Applications of stacks
Used in browser navigation history.
Used to implement recursion.
Used in stack-based memory allocation.
 Stack push and pop - Source: Wiki
Stack push and pop - Source: Wiki
Queue
Similar to stacks, queues are another type of linear data structure based on either arrays or linked lists. The characteristic that differentiates a queue data structure from a stack is that a queue is based on the principle First-In-First-Out (FIFO), where an element that enters the queue first, will leave first.
A real-life analogy of the “queue” data structure would be a line of people waiting to purchase a movie ticket, also known as a “queue.”
 Photo by Levi Joneson Unsplash
Photo by Levi Joneson Unsplash
Basic queue operations
Enqueue: Insert element to the end of the queue.Dequeue: Remove an element from the front of the queue.Top/Peek: Returns the element from the front of the queue without removing.isEmpty: Checks whether the queue is empty.
Applications of queues
Serve multiple requests on a single shared resource.
Manage threads in multi-threaded environments.
Load balancing.
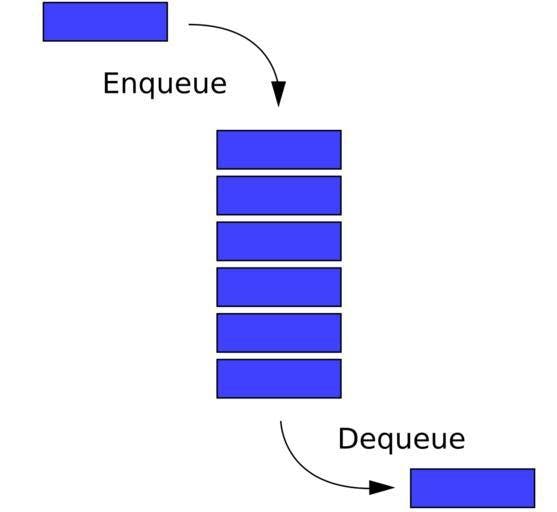 Enqueue and Dequeue operations— Source: SnappyGoat
Enqueue and Dequeue operations— Source: SnappyGoat
Graph
A graph is a data structure that is an interconnection of nodes. These nodes are also referred to as vertices. A pair (x,y) is called an edge, which indicates that vertex x is connected to vertex y. An edge may indicate a weight/cost value, which is the cost of traversing through that path — between two vertices.
Key terms
Size: Number of edges in the graph.
Order: Number of vertices in the graph.
Adjacency: When two nodes are connected by the same edge.
Self-looped: A vertex that is connected to itself by an edge.
Isolated: A vertex that is not connected to any other vertex.
There are mainly two types of graphs. These graphs are differentiated mainly because of the direction of the path between two vertices.
Directed graphs: Graphs where all edges have directions indicating the starting and ending point(vertex)
Undirected graphs: Graphs where the edges have no directions which allow traversals to happen from any direction.
Commonly-used graph traversal algorithms
Breadth First Search (BFS): A technique based on vertices to find the shortest path in a graph.
Depth First Search (DFS): A technique based on edges.
Basic Graph Operations
Add vertex: Add a vertex to a graph
Add edge: Add an edge between two vertices
Display: Display a vertex
Total cost of traversal: Find the total cost of a path by traversing
Applications of Graphs
Used to represent the flow of computation.
Used in resource allocation by the operating system.
Implementation of friend suggestion algorithms used by Facebook.
Calculation of the shortest path between two locations (Google Maps).
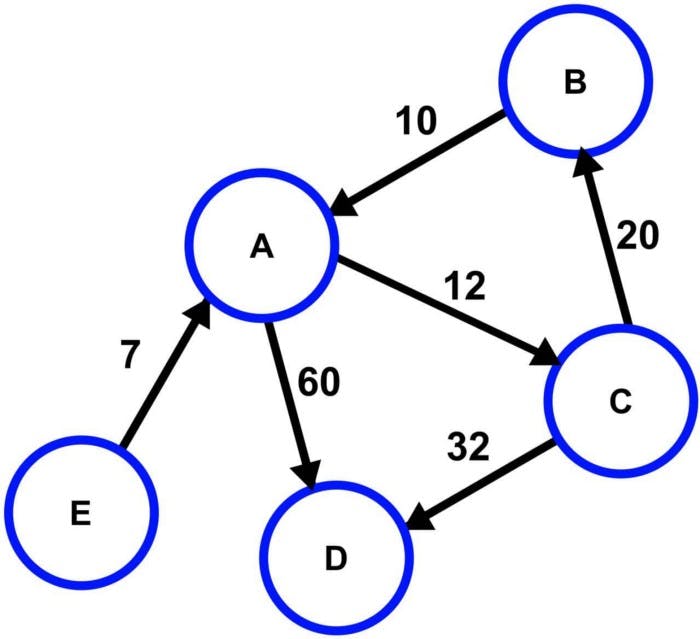 Directed graph with cost — Source: Wiki
Directed graph with cost — Source: Wiki
Tree
A tree is a hierarchical data structure consisting of vertices (nodes) and edges that connect them. Trees are often used in AI and complex algorithms as they provide an efficient approach to problem-solving. A tree is a special type of graph that does not contain any cycles. Some people argue that trees are totally different from graphs but these arguments are subjective.
 Photo by Fabrice Villard on Unsplash
Photo by Fabrice Villard on Unsplash
There are several types of trees.
N-ary Tree
Balanced Tree
Binary Tree
Binary Search Tree (BST)
AVL Tree
Red Black Tree
2–3 Tree
BSTs are a special variant of Binary trees and these two are the most commonly used tree types.
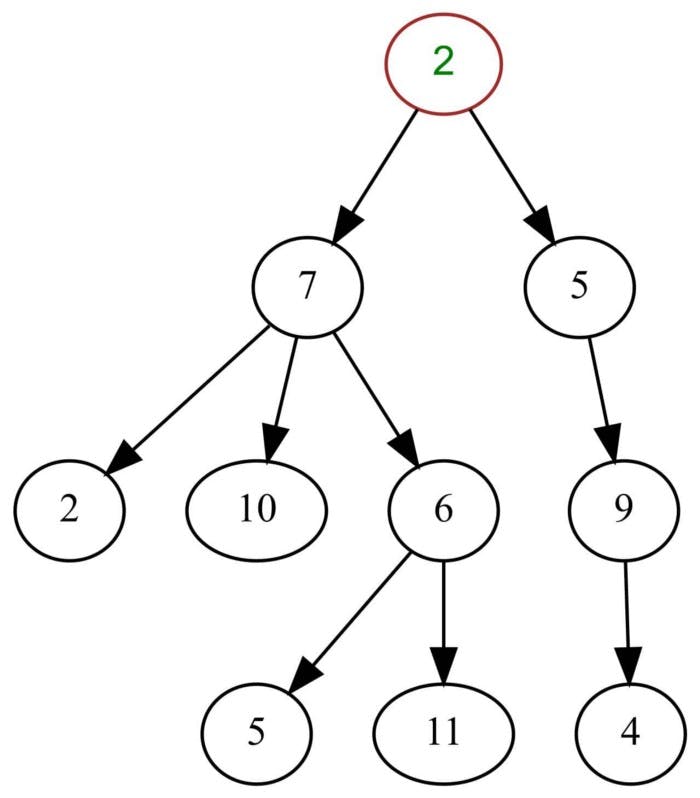 A simple tree — Source: Wiki
A simple tree — Source: Wiki
Basic BST operations
Insert: Insert an element into a tree.Search: Search for an element within a tree.PreorderTraversal: Traverse a tree in a pre-order manner.InorderTraversal: Traverse a tree in an in-order manner.PostorderTraversal: Traverse a tree in a post-order manner.
Applications of trees
Representation of an organization
Representation of a computer file system
Representation of a chemical formula
Used in decision trees
Used by JVM (Java Virtual Machine) to store Java objects
Hash Table
Hash Table data structure stores data in key-value pairs. This means that each key in the hash table has a corresponding value associated with it. This simple layout makes hash tables very efficient in the insertion and searching of data, regardless of the size of the table.
Although this is similar to a regular key-value pair data store, the generation of the keys makes hash tables unique. Keys are generated with a special process called hashing.
Hashing (hash function)
Hashing is a process that converts a key with a hash function in order to receive a hashed key. This hash function determines the index of the table or structure where the value should be stored.
h(k) = k % m
h: Hash function
k: Key of which the hash value should be determined
m: Size of the hash table.
For example, consider using a hash function, k%17. If the original key is 20, the hashed key would 20%17=3. This means that the value would be stored in index 3 of our hash table.
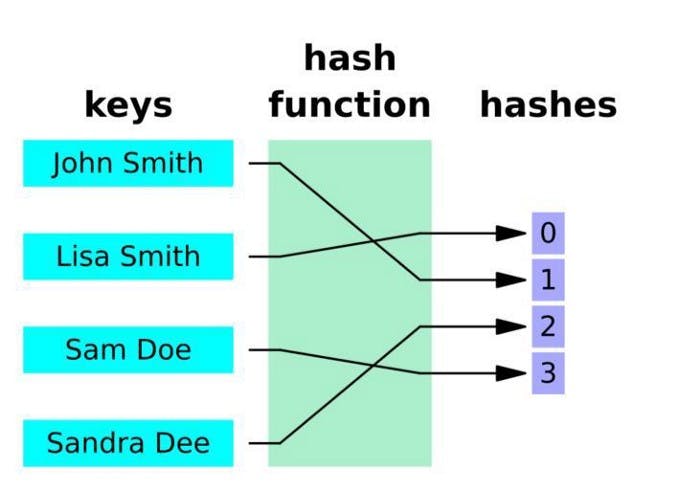 Hash function for keys — Source: SnappyGoat
Hash function for keys — Source: SnappyGoat
Why do we hash?
Sometimes people might wonder why should we go through this additional process of hashing when we can simply map the values directly with the key. Although direct mapping is simple, it might not be an efficient solution when used with a large data set. With hashing, we can achieve a near-constant time of O(1).
Collisions
Since a common hash function is used for converting all keys, there’s the possibility of collisions. Let’s have a look at the below example considering our hash function k%17.
When k = 18, h(18) = 18%17 = 1.
When k = 20, h(20) = 20%17 = 3.
When k = 35, h(35) = 35%17 = 1.
As seen above, when the keys are 18 and 35, there is a collision happening as both keys direct to index 1.
Collisions can be resolved by using strategies such as separate chaining and open addressing.
Basic hash table operations
Search: Search for an element within the hash tableInsert: Insert an element into the hash tableDelete: Remove an element from the hash table
Applications of hash tables
Used in database indexing
Used in spell checkers
Used in the implementation of the Set data structure
Used in caches
Conclusion
It’s essential for developers to know at least the basics of these data structures as, with proper implementation, they can increase the efficiency of your applications.
Thank you for reading and happy coding!
